Validation of Assay Methods – PharmaG33k’s Blog

Access the free and open tool for validating dosing methods -> ValidR

Validation of Assay Methods: Philosophy and Standardization

The validation of assay methods is essential to ensure the reliability of analytical results across various fields, particularly in the pharmaceutical industry. Although many regulations (e. g. ICH, EMEA, FDA) define general validation criteria, they often lack detailed experimental protocols and remain limited to conceptual guidance.

The International Council for Harmonisation (ICH) guideline Q2(R2) defines validation parameters such as precision, accuracy, and specificity. However, the ICH does not prescribe specific statistical approaches, leaving users to determine the most suitable methods based on their analytical context.

To address this gap, the SFSTP (French Society for Pharmaceutical Sciences and Techniques) published a series of guides^1–4 aimed at standardizing the practical application of these recommendations. These works introduced the concept of the accuracy profile, based on total error. This approach simplifies analytical validation while controlling the risks associated with the use of validated methods.

The Philosophy of Assay Method Validation

The validation of assay methods is grounded in a risk-based analytical philosophy, as emphasized by the SFSTP. The central objective is to ensure that the method delivers reliable results, while minimizing two major risks:

accepting an incorrect result (false positive),
rejecting a correct result (false negative).

A validated method must therefore guarantee, with a defined level of confidence, that each assay correctly classifies out-of-specification and in-specification results.

Figure 1: Graphical representation of a distribution with mean = 100 and CV = 10%

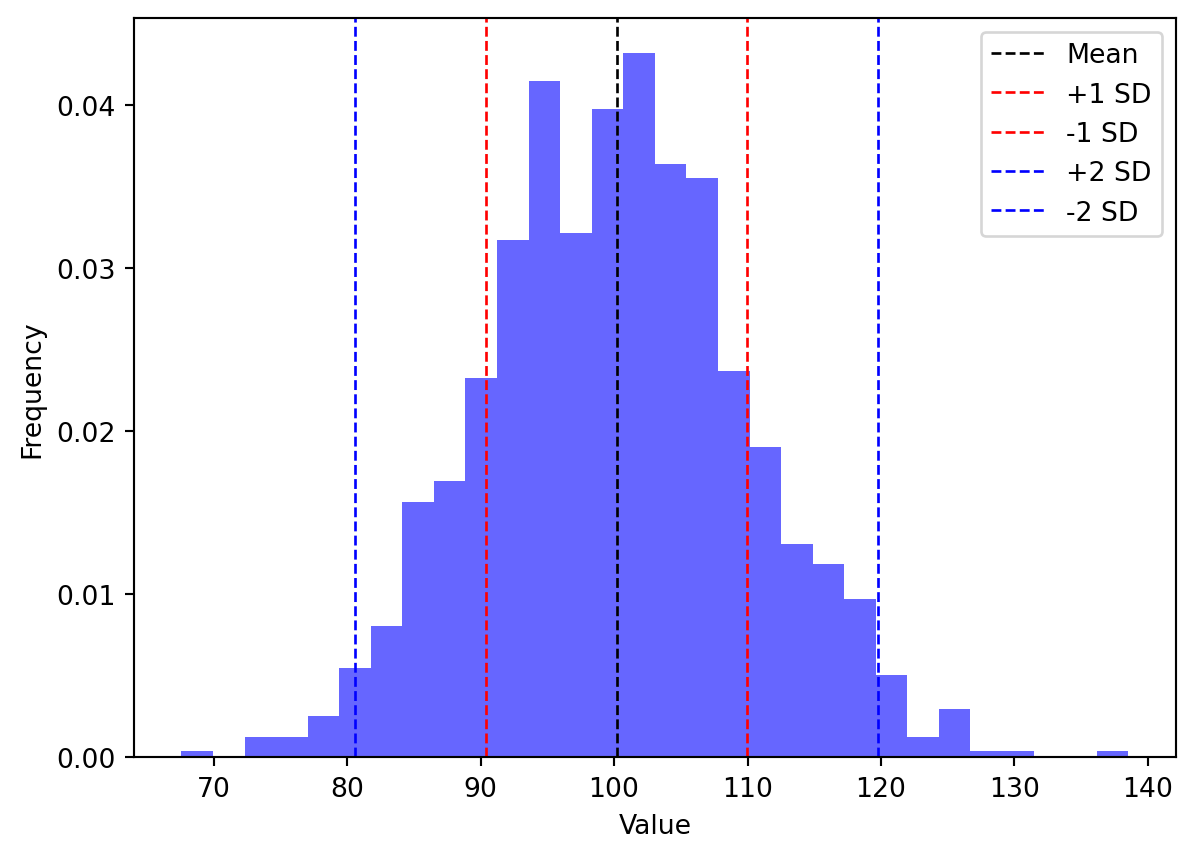
As illustrated in Figure 1, relying solely on the coefficient of variation (CV) as an acceptance criterion can be misleading and expose analytical methods to significant risks. While the CV provides a useful measure of relative variability, it obviously fails to account for systematic bias or the absolute position of results relative to specification limits.

Moreover, consider a method with a mean recovery of 100% and a CV of 10% (i. e. sd = 10). At first glance, this may seem acceptable. However, if the acceptance limits are set at ±10% of the target value (e.g., 90–110% for a target of 100%), the distribution of results may still include a substantial proportion of values outside these limits. And the more the CV is close to acceptance limits, the more the risk of out-of-specification results is high.

Note

Assuming a Normal distribution :

only 68.2% of datas fall in \([\mu - \sigma, \mu + \sigma]\).
95.4% of datas fall in \([\mu - 2\sigma, \mu + 2\sigma]\)
99.7% of datas fall in \([\mu - 3\sigma, \mu + 3\sigma]\).

In other words, the CV alone does not guarantee that future results will comply with specification limits. It only describes variability relative to the mean, not relative to the acceptance criteria. This is why the SFSTP accuracy profile provides a more robust framework for method validation.

Important

In a pharmaceutical context, it is paramount to ensure that the results meet the acceptability criteria in the majority of cases rather than on average. It is difficult to imagine saying that a batch is on average acceptable or that 30% of the units may not be compliant. This critical requirement underscores the necessity of robust validation methodologies that go beyond traditional mean-based assessments, emphasizing population coverage and risk mitigation in analytical decision-making.

Accuracy profile

This approach evaluates how the entire distribution of results aligns with predefined acceptance limits. The accuracy profile thus provides a clear visualization of the expected population of analytical results, accounting for total error, and enables a more meaningful estimation of the risk associated with method use, especially near specification limits.

The accuracy profile is based on the β-tolerance interval, a statistical interval designed to estimate where a specified proportion (β) of a population’s values are expected to fall, with a given level of confidence (1−α), based on samples. This approach evaluates both precision and bias simultaneously, allowing for the estimation of the β-proportion of all future results that will fall within the fixed acceptance limits. Unlike traditional methods that rely solely on mean bias and coefficient of variation, this proposal now emphasizes inference based on robust design and sampling strategies.

The SFSTP’s β-tolerance interval approach incorporates two dimensions:

the proportion covered (β, e.g., 95% of results),
the statistical confidence (1−α, e.g., 90% certainty).

Tip

In statistics, there are three main types of intervals:

Confidence interval (CI): estimates the true mean of a population with a given level of confidence. It reflects the uncertainty of the mean.
Prediction interval (PI): predicts where a future individual observation is likely to fall, taking into account both mean uncertainty and data variability.
Tolerance interval (TI): defines the range within which a specified proportion (β) of the population is expected to fall, with a given confidence level (1−α).

Together, these three intervals illustrate the progression from estimation (confidence), to prediction, to population coverage (tolerance).

In this perspective, the SFSTP approach emphasizes evaluation under real-use conditions. This methodology allows analysts to predict the distribution of future analytical results and determine whether the method will meet acceptance criteria in routine practice. By applying appropriate statistical tools, the aim is to reduce the probability of decision errors—rejecting a suitable method or accepting an inadequate one.

The need for an open-access and free tool

While the SFSTP philosophy defines the conceptual and statistical framework for assessing analytical method reliability, its application often requires advanced statistical knowledge and computational effort. To make this approach accessible to all analysts, the ValidR tool was developed as a practical implementation of the SFSTP paradigm, automating the computation of accuracy profiles and β-tolerance intervals, and ensuring consistent, transparent application of risk-based validation principles.

Why using ValidR?

It’s free as in free (and open-source, because why pay for something that’s already free? 😉)
It’s open source, so that you can review the code, validate it (but it was already performed on multiple datasets), find bugs, or suggest improvements. You can fork it on github, you can download it… just look at my github (link in the menubar)
It produces an HTML interactive report you can share with your colleagues or reviewers.
You’re name is not David Goodenough

References

Hubert, P. et al. Harmonization of strategies for the validation of quantitative analytical procedures. A SFSTP proposal–part i. J Pharm Biomed Anal 36, 579–586 (2004).

Hubert, P. et al. Harmonization of strategies for the validation of quantitative analytical procedures. A SFSTP proposal–part II. J Pharm Biomed Anal 45, 70–81 (2007).

Hubert, P. et al. Harmonization of strategies for the validation of quantitative analytical procedures. A SFSTP proposal–part III. J Pharm Biomed Anal 45, 82–96 (2007).

Hubert, P. et al. Harmonization of strategies for the validation of quantitative analytical procedures: A SFSTP proposal part IV. Examples of application. J Pharm Biomed Anal 48, 760–771 (2008).